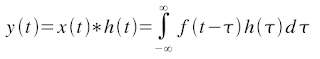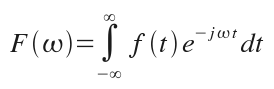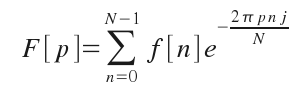The continuous form of the convolution is given by:
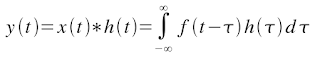
So, the discrete form is given by:
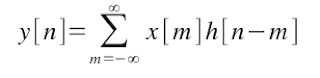
If x[n] and h[n] are limited in the time ({x[n] = 0 if n <> Xn} and {h[n] = 0 if n <> Hn}), then the convolution is implemented as follow:
Let's suppose Xn > Hn (if Hn > Xn, the analysis is the same).
The equation is separated in three cases:
Case 1
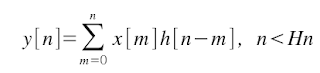 Case 2
Case 2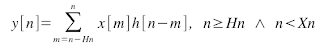 Case 3
Case 3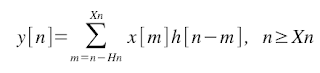 Any other situation, y[n] = 0.
Any other situation, y[n] = 0.If you make an analysis in y[n], you'll see that y[n] = 0, if n <> Xn + Hn - 1.
Some other properties of the discrete convolution are the same than the continuous convolution:
- x[n] * h[n] = h[n] * x[n];
- x[n]*(h1[n]*h2[n]) = (x[n]*h1[n])*h2[n];
- x[n]*(h1[n] + h2[n]) = x[n]*h1[n] + x[n]*h2[n];
- a(x[n]*h[n]) = (ax[n])*h[n] = x[n]*(ah[n]), a is real;
- x[n]*d[n] = x[n], d[n] = 1 if n = 0 and d[n] = 0 if n is not null;
- x[n]*xi[n] = d[n], xi[n] is the inverse of x[n].
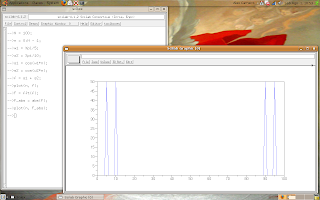
Say me what happens.